Crecemos y Aprendemos Juntos Volumen de cuerpos geométricos

Maestro San Blas Los cuerpos geométricos
VOLÚMENES DE LOS CUERPOS GEOMÉTRICOS. Cuando estudiamos las áreas hablábamos de dos dimensiones: largo y ancho. El producto de los valores largo X ancho nos da el área. Para calcular un volumen necesitamos tres dimensiones: largo, ancho y alto. El producto de los valores largo X ancho X alto nos da el volumen.

FORMULAS+DE+AREAS+Y+VOLUMENES+DE+CUERPOS+GEOMETRICOS.gif (1260×1600) Teaching math, Math
En este vídeo mostramos varios ejemplos de cálculo de área y volumen en cuerpos geométricos compuestos, es decir, formados por la combinación de más de cuerpo.

Cuerpos Geométricos. ¿Qué son?. Ejemplos y ejercicios resueltos
El volumen total de cuerpos geométricos, como el ortoedro y el cubo , se halla multiplicando sus tres dimensiones: largo, ancho y alto. De igual manera, el volumen del cilindro y la pirámide se halla multiplicando el área de las bases por su altura. 1. Comprender el concepto de volumen de los cuerpos. 2. Relacionar las unidades

Fórmulas de área y volumen de cuerpos geométricos
Comprobar. Explicación. Ahora podemos calcular el volumen de la pirámide. Combinemos las dos mitades de pirámide y obtengamos el volumen de la pirámide entera. El volumen de toda pirámide es á 1 3 ( área de la base. rea de la base) ( altura) .

Volúmenes de cuerpos geométricos
El volumen de un cubo se calcula multiplicando el área de su base cuadrada por la altura del cubo. Por lo tanto, el volumen de un cubo es igual a la longitud de su lado (o arista) elevada al cubo. Así pues, la fórmula del volumen de un cubo es la siguiente: Ver: Ejemplo del cálculo del volumen de un cubo.
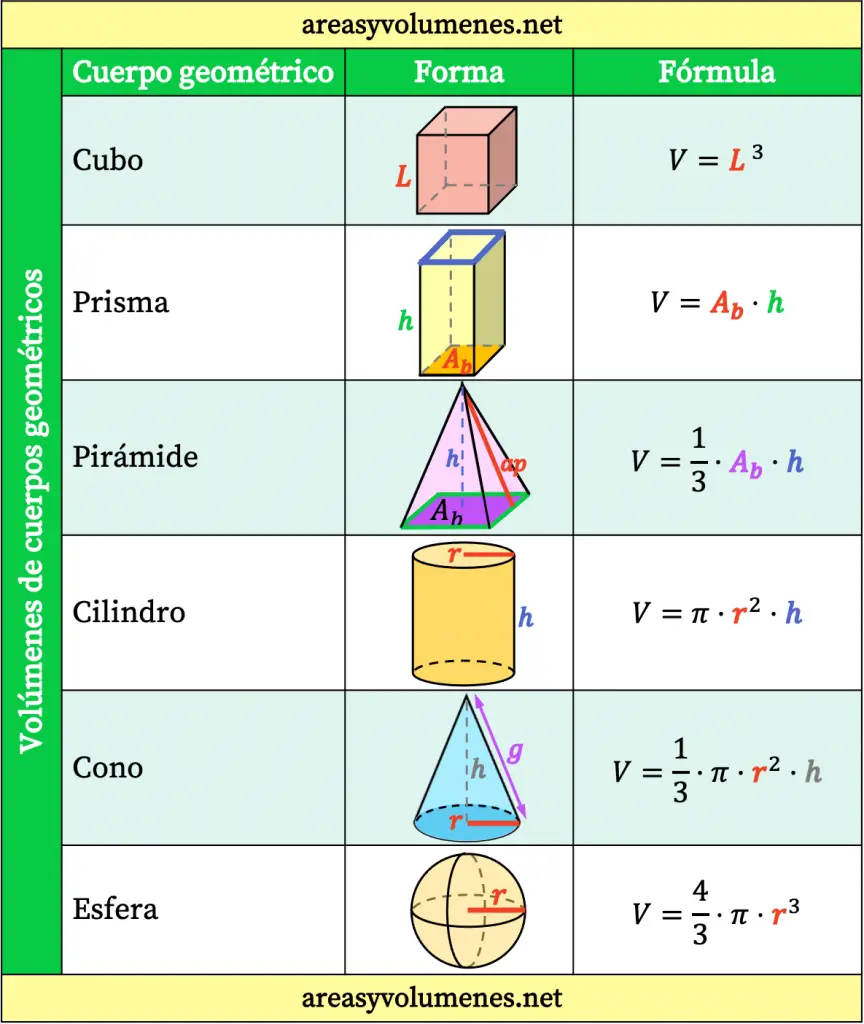
Fórmulas de Volúmenes de Cuerpos Geométricos
Los cuerpos geométricos tienen las siguientes características: Tienen tres dimensiones: largo, ancho y alto. Ocupan un volumen en el espacio. Se dividen en poliedros (con todas sus caras planas) y cuerpos redondos (con al menos una cara curva). Los elementos de los cuerpos geométricos incluyen caras, aristas y vértices.

Crecemos y Aprendemos Juntos Volumen de cuerpos geométricos
Main content: Volumen de los cuerpos geométricos (2011602) Ejercicios y actividades interactivas para identificar los diferentes tipos de cuerpos geométricos, su desarrollo y aplicación de las fórmulas para averiguar su volumen.

Sexto U8 1.6 Volumen de cuerpos geométricos compuestos completando YouTube
Definición: Un cuerpo geométrico es un elemento que existe en la realidad o que somos capaces de concebir, el cual ocupa un volumen en el espacio, es decir, tiene tres dimensiones (ancho, alto y largo) a diferencia de las figuras, las cuales no tienen volumen. Clasificación: Hay dos tipos de cuerpos geométricos: los poliedros y los no.

AREAS Y VOLUMENES DE CUERPOS GEOMETRICOS PDF
Baricentro: su distancia al vértice de un tetraedro es 3/4 de h T y su distancia a una cara es 1/4 de h T, aquí h T = altura del tetredro. Área: a 2 ×3 0.5, cuatro veces el área de cada cara que es un triángulo regular. Volumen del tetraedro: a 3 ×2 0.5 ÷12; a = arista; volumen = 1/3 base x altura.
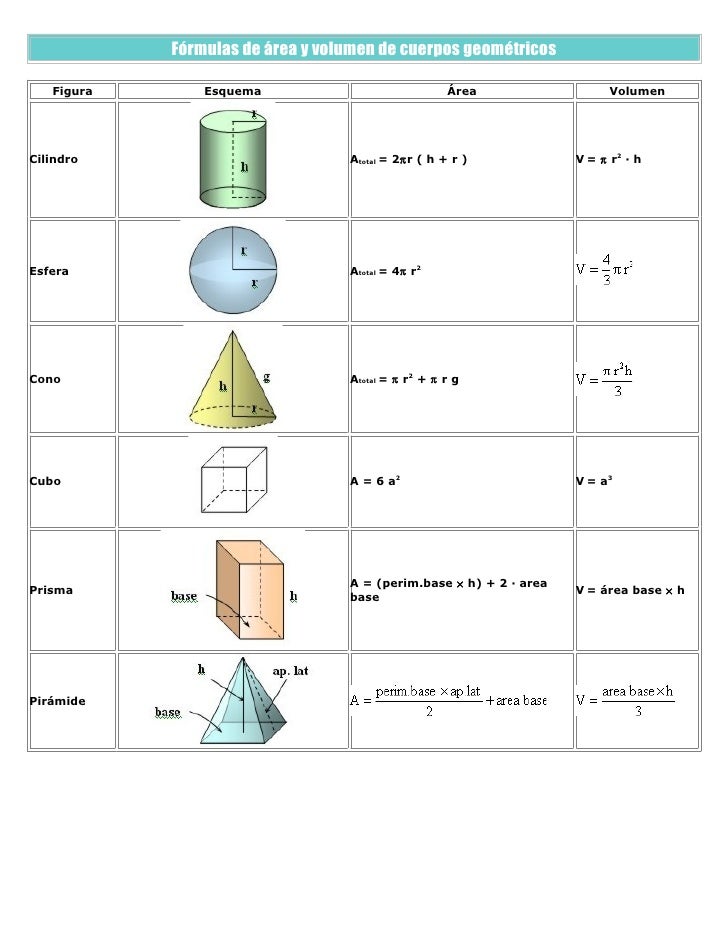
Fórmulas De área Y Volumen De Cuerpos Geométricos
2- Definición de volumen y capacidad. - Volumen: es la medida del espacio que ocupa un cuerpo. - Capacidad: es la medida del volumen que puede contener un cuerpo. Como en genera estas medidas son iguales, se suele calcular la capacidad mediante la fórmula del volumen. La medida universal del volumen es el metro cúbico ( m3 ), existiendo los.

Volumen de cuerpos geométricos Volumen de cuerpos geometricos, Actividades de geometría
8. Calcula el área y el volumen de estos cuerpos geométricos: 2 A ortoedro 766cm 3 V ortoedro 1260cm 425 2 A cono 5 314 25 S cm 3 cono cm 3 V S 2 A cilindro 252S cm 3 V cilindro 540S cm 9. Halla el área y el volumen de este prisma cuyas bases son triángulos equiláteros: 2 A prisma 405 9 60,75 cm 3 prisma cm 2 135 60,75 V 2 10. Calcula.

CÁLCULO DEL VOLUMEN EN CUERPOS GEOMÉTRICOS
Observa que cualquier cara de un prisma rectangular puede ser su base, siempre que la altura del prisma se mida perpendicularmente a esa cara. l h w. Á á á á Volumen prisma rectangular = ( Área. rea rectángulo. rect ngulo) ⋅ ( altura) = ( ( base del rectángulo. base del rect ngulo) ( altura del rectángulo. altura del rect ngulo)) ⋅.

Ficha online de Volumen de los cuerpos geométricos para primero. Puedes hacer los ejercicios
Áreas y volúmenes de cuerpos geométricos. Cómo calcular el área y el volumen de pirámides, conos y diversos prismas, explicado todo paso a paso.Área y volume.

FORMULARIOS DE GEOMETRÍA para Primaria y Secundaria Imagenes Ed… Volumen de figuras
ser capaz de encontrar el volumen de algunos objetos geométricos comunes. Muy a menudo es necesario multiplicar un número denominado por otro. Para ello, multiplicamos las partes numéricas juntas y las partes unitarias juntas. Por ejemplo, 8 in. ⋅ 8 in. = 8 ⋅ 8 ⋅ in. ⋅ in. = 64 in.2. 4 mm ⋅ 4 mm ⋅ 4 mm = 4 ⋅ 4 ⋅ 4 ⋅ mm ⋅.
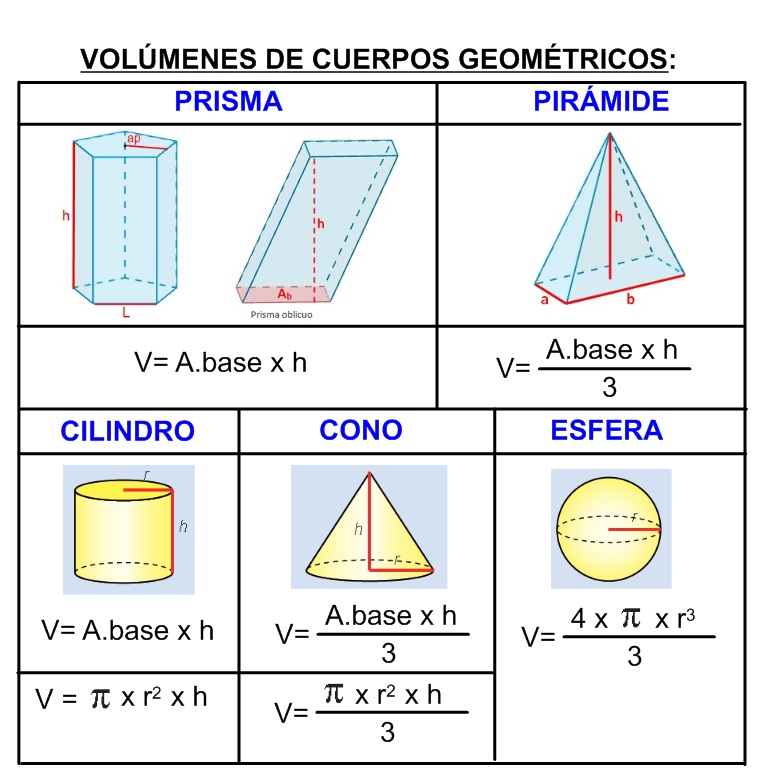
5º y 6º Educación Primaria VOLÚMENES DE LOS CUERPOS GEOMÉTRICOS
Por lo tanto, la diferencia entre el área y el volumen es el número de dimensiones. El área es el espacio de dos dimensiones que ocupa una figura, en cambio, el volumen es el espacio de tres dimensiones que ocupa un cuerpo geométrico. Por ejemplo, una viga redonda en posición vertical es un cilindro que tiene un gran volumen porque es un.

Volumen de cuerpos geométricos YouTube
Cuando se trata de un cuerpo geométrico como los ya mencionados, el volumen se calcula a través de la fórmula adecuada, midiendo las dimensiones indicadas por la fórmula. Por ejemplo, si se quiere conocer el volumen de una esfera, es necesario medir su diámetro y con ello se conoce su radio, que es la mitad. Si se trata de una caja.